degree calculator right triangle

Right Triangle Calculator

Please provide 2 values below to calculate the other values of a right triangle. If radians are selected as the angle unit, it can take values such as pi/3, pi/4, etc.

Related Triangle Calculator | Pythagorean Theorem Calculator

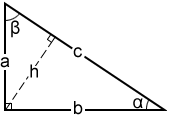
Right triangle

A right triangle is a type of triangle that has one angle that measures 90°. Right triangles, and the relationships between their sides and angles, are the basis of trigonometry.

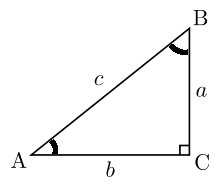
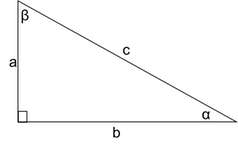
In a right triangle, the side that is opposite of the 90° angle is the longest side of the triangle, and is called the hypotenuse. The sides of a right triangle are commonly referred to with the variables a, b, and c, where c is the hypotenuse and a and b are the lengths of the shorter sides. Their angles are also typically referred to using the capitalized letter corresponding to the side length: angle A for side a, angle B for side b, and angle C (for a right triangle this will be 90°) for side c, as shown below. In this calculator, the Greek symbols α (alpha) and β (beta) are used for the unknown angle measures. h refers to the altitude of the triangle, which is the length from the vertex of the right angle of the triangle to the hypotenuse of the triangle. The altitude divides the original triangle into two smaller, similar triangles that are also similar to the original triangle.

If all three sides of a right triangle have lengths that are integers, it is known as a Pythagorean triangle. In a triangle of this type, the lengths of the three sides are collectively known as a Pythagorean triple. Examples include: 3, 4, 5; 5, 12, 13; 8, 15, 17, etc.

Area and perimeter of a right triangle are calculated in the same way as any other triangle. The perimeter is the sum of the three sides of the triangle and the area can be determined using the following equation:

Special Right Triangles

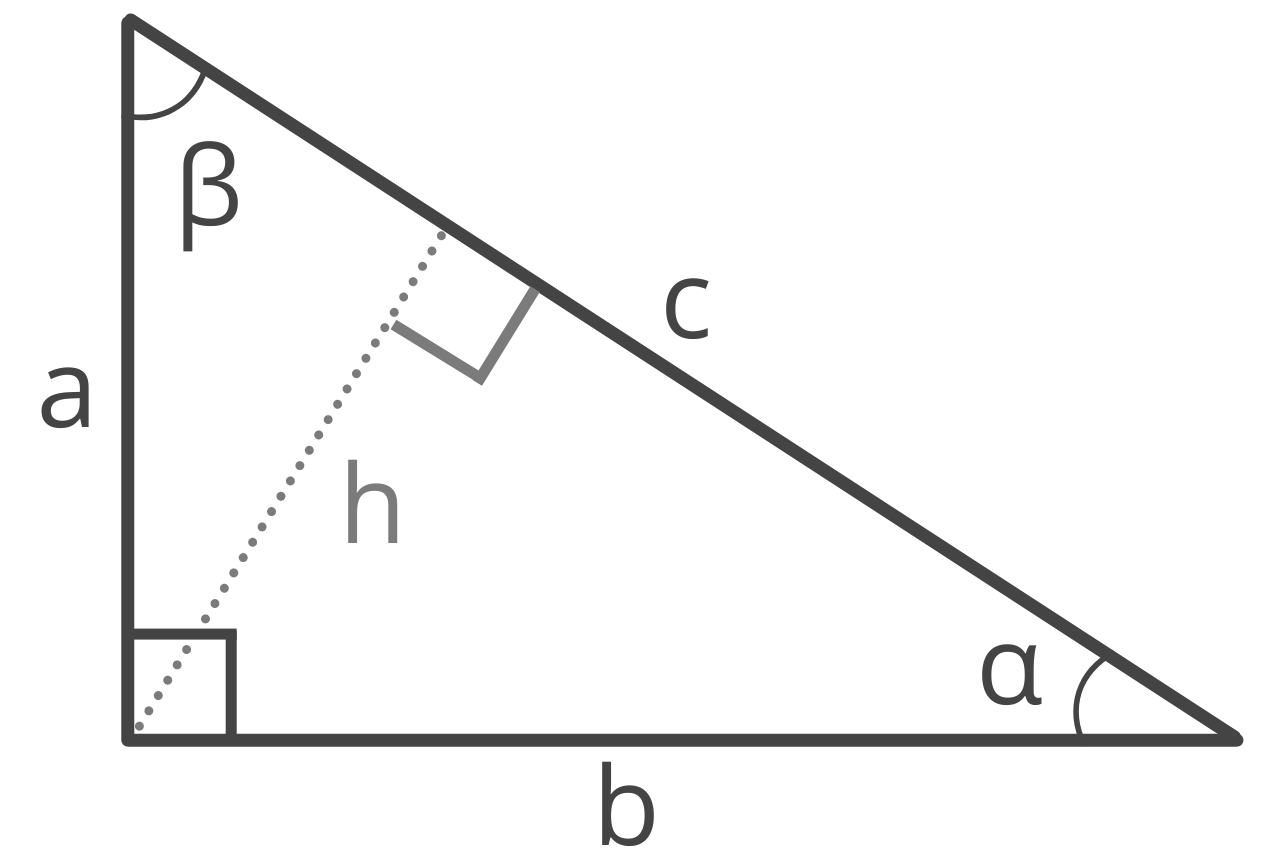
30°-60°-90° triangle:

The 30°-60°-90° refers to the angle measurements in degrees of this type of special right triangle. In this type of right triangle, the sides corresponding to the angles 30°-60°-90° follow a ratio of 1:√ 3 :2. Thus, in this type of triangle, if the length of one side and the side's corresponding angle is known, the length of the other sides can be determined using the above ratio. For example, given that the side corresponding to the 60° angle is 5, let a be the length of the side corresponding to the 30° angle, b be the length of the 60° side, and c be the length of the 90° side.:

Angles: 30°: 60°: 90°

Ratio of sides: 1:√ 3 :2

Side lengths: a:5:c

Then using the known ratios of the sides of this special type of triangle:

As can be seen from the above, knowing just one side of a 30°-60°-90° triangle enables you to determine the length of any of the other sides relatively easily. This type of triangle can be used to evaluate trigonometric functions for multiples of π/6.

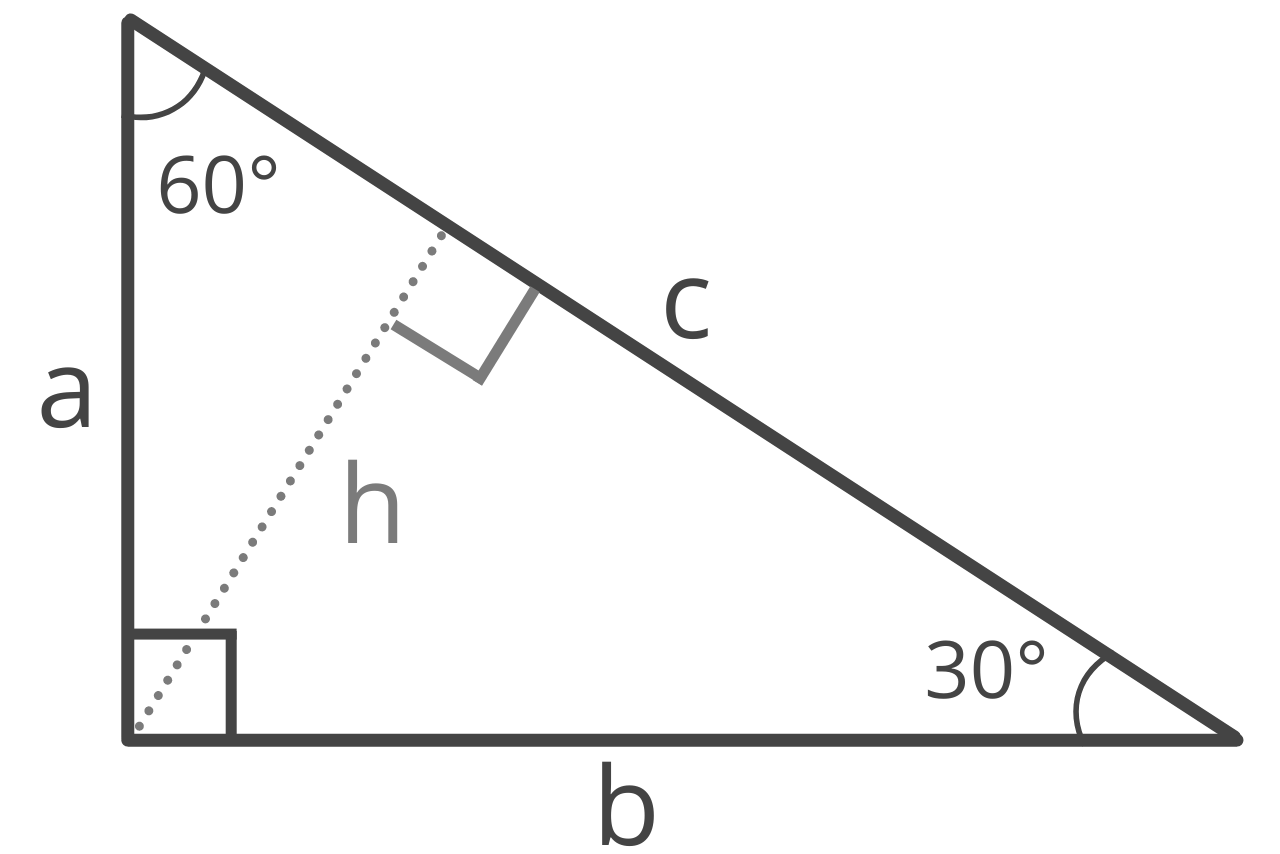
45°-45°-90° triangle:

The 45°-45°-90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°-45°-90°, follow a ratio of 1:1:√ 2 . Like the 30°-60°-90° triangle, knowing one side length allows you to determine the lengths of the other sides of a 45°-45°-90° triangle.

Angles: 45°: 45°: 90°

Ratio of sides: 1:1:√ 2

Side lengths: a:a:c

Given c= 5:

45°-45°-90° triangles can be used to evaluate trigonometric functions for multiples of π/4.

Right Triangle Calculator

Enter any two known values for a right triangle below to calculate the edge lengths, altitude, angles, area, perimeter, inradius, and circumradius.

Have a Question or Feedback?

Right triangle properties:, type of right triangle:.

Chevron Down Icon scroll down

On this page:

What is a right triangle, types of right triangles, how to find the hypotenuse of a right triangle, how to find a missing side, how to find the angle of a right triangle, how to find the area of a right triangle, method one: using two legs, method two: using hypotenuse and one leg, method three: using one leg and one angle, how to find the perimeter, special right triangles, formulas for 30 60 90 right triangles, formulas for 45 45 90 right triangles.

Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.

Full bio Chevron Right Icon

Zach is a former math teacher with a Master's degree in education and a Bachelor's degree in mathematics, and is currently pursuing his PhD.

A right triangle , sometimes called a right-angled triangle, is a triangle that has one interior angle equal to exactly 90 degrees, forming what is called a right angle.

The sides adjacent to the right angle are referred to as legs a and b , and are also often referred to as the base and height. The calculator uses the term height to represent the altitude of a triangle.

The side opposite the right angle is called the hypotenuse c .

Right triangles can be broken into two categories: isosceles and scalene.

An isosceles right triangle is a special isosceles triangle that has two angles that are 45 degrees and legs a and b of equal length.

A scalene right triangle is one where all the angles are unequal, and all the sides are unequal in length.

To calculate the length of the hypotenuse in a right triangle when you know the length of the two legs, you can use the Pythagorean theorem .

The Pythagorean theorem states that side a squared plus side b squared is equal to side c squared. Note, keep in mind that sides a and b specifically refer to the legs, and side c refers to the hypotenuse.

a² + b² = c²

To find the hypotenuse, take the square root of the sum of a squared and b squared.

c = a² + b²

So, the value of the hypotenuse is equal to the square root of leg a squared plus leg b squared.

For example, let’s find the hypotenuse c for a triangle with leg a = 3 and leg b = 4.

3² + 4² = c² 9 + 16 = c² 25 = c² 25 = c 5 = c

So, the hypotenuse c is equal to 5 for a right triangle with legs a = 3 and b = 4.

To calculate the length of a missing side, you can use a known side and the hypotenuse and rearrange the Pythagorean theorem to solve the missing variable.

For instance, to find leg b , rearrange the Pythagorean theorem to solve for b by subtracting a² from both sides.

a² + b² = c² a² + b² – a² = c² – a² b² = c² – a²

Then take the square root of the right side of the equation to isolate the missing leg, which is b in this example.

b = c² – a²

So, the value of the missing leg b is equal to the square root of the hypotenuse c squared minus the length of the known leg a squared.

If you know the lengths of two sides of a right triangle, then you can determine the interior angles using the trigonometric functions sine , cosine , and tangent . These are usually shortened to sin , cos , and tan .

To find the angle given two side lengths, you can use the following formulas:

sin(θ) = opposite ÷ hypotenuse cos(θ) = adjacent ÷ hypotenuse tan(θ) = opposite ÷ adjacent

In a right triangle, the adjacent side to θ is the side of the triangle that forms part of the angle θ but is not the hypotenuse. The opposite side to θ is the side that does not form part of the angle θ .

To find one of the angles, choose the formula that can be used given the two known side lengths, then substitute the known values in the formula and solve.

For example, let’s find the angle of a triangle if the adjacent side length is 7 and the hypotenuse is 15.

Start by choosing the equation using adjacent and hypotenuse: cos(θ) = adjacent ÷ hypotenuse

cos(θ) = 7 ÷ 15 cos(θ) = 0.4667 θ = cos -1 (0.4667) θ = 62.18°

So, for a right triangle with angle θ , with an adjacent side length of 7 and hypotenuse of 15, the angle θ is 62.18°. Note, in the above example, the inverse of cosine was used in the second to last question to isolate θ .

You can find the remaining angle in a few ways. The first way is to repeat using the same method as before, but with a different formula to find the remaining angle.

You can also use the special rule of triangles where the sum of all angles must equal 180°. Subtract 90° (because this is a right triangle, we know one of the angles is 90°) and the angle you just found from 180 to find the missing angle.

You can use the mnemonic SOHCAHTOA to help remember the equations above.

If you split SOHCAHTOA into three parts, each part represents one of the formulas, where each letter is the first letter in the part of the equation.

SOH · CAH · TOA

SOH: s in(θ) = o pposite ÷ h ypotenuse CAH: c os(θ) = a djacent ÷ h ypotenuse TOA: t an(θ) = o pposite ÷ a djacent

Learn more about using this mnemonic on our SOHCAHTOA calculator .

There are a few methods to find the area of a right triangle.

If you know the length of the two legs in a right triangle, then you can find the area using the formula:

A = 1 / 2 a × b

The area A of a right triangle is equal to one-half times leg a times leg b .

If you know the hypotenuse and one of the legs, then you can use a variation of the Pythagorean theorem to find the area:

A = a × 1 / 2 c² – a²

The area A of a right triangle is equal to leg a times 1/2 times the square root of the hypotenuse c squared times minus leg a squared. Notice the √(c² – a²) portion of this formula is simply the Pythagorean theorem isolated for b .

If you know the length of one leg and the value of an adjacent angle, then you can use the tangent function to find the area.

Given the value of leg a and angle β , find the area using the following formula:

A = a² × tan(β) / 2

Given the value of leg b and angle α , find the area using the following formula:

A = b² × tan(α) / 2

The area A of a right triangle is equal to leg a squared times one-half the tangent of angle β , or leg b squared times one-half the tangent of angle α .

Keep in mind that in the above formulas, angle β must be adjacent to leg a , and angle α must be adjacent to leg b .

The formula to find the perimeter of a right triangle is:

perimeter = a + b + c

The perimeter is equal to leg a plus leg b plus hypotenuse c .

You can use the formulas above to find the lengths of the missing leg or hypotenuse if any are missing.

There are a few types of special right triangles, which are triangles that have specific proportions. These special right triangles also have formulas to simplify solving them.

A 30 60 90 triangle is a special right triangle with 30° and 60° interior angles adjacent to the right 90° angle.

Given the length of leg b (the side opposite the 60° angle), the formula to find the length of a is:

a = b × √3 / 3

The length of leg a is equal to b times the square root of 3, divided by 3.

Given the length of leg a (the side opposite the 30° angle), the formula to find the length of b is:

b = a√3

The length of leg b is equal to a times the square root of 3.

Hypotenuse c

In the case of a 30 60 90 right triangle, the length of the hypotenuse is always equal to two times the length of the shortest leg. So, given the length of the short leg a , the formula to find the hypotenuse is:

The length of c is equal to 2 times a .

A 45 45 90 triangle is a special right isosceles triangle with 45° interior angles adjacent to the 90° right angle.

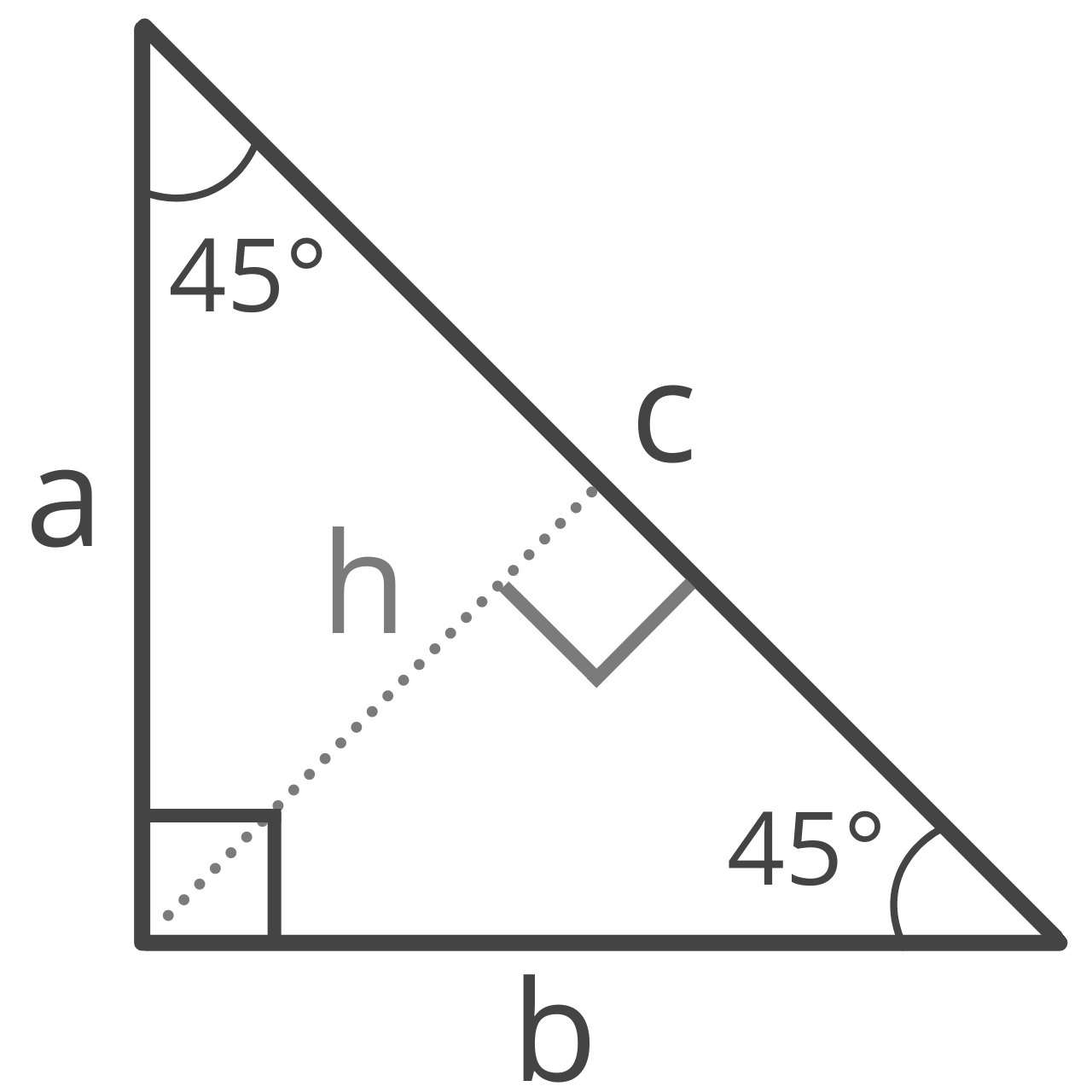
Legs a & b

Given the hypotenuse, you can find the length of the legs a and b in a 45 45 90 triangle using the formula:

a = b = c√2 / 2

The length of legs a and b are equal to hypotenuse c times the square root of 2, divided by 2.

Since it is an isosceles triangle , both legs are the same length, so there is a special formula to find the length of the hypotenuse.

c = a√2

The length of side c is equal to the length of side a times the square root of 2.

There is also a special formula to find the area of a 45 45 90 right triangle:

A = a² / 2

The area A of the right triangle is equal to the length of leg a squared, divided by 2.

Recommended Triangle Resources

• Triangle Area Calculator Right Arrow Icon
• SOHCAHTOA Calculator Right Arrow Icon
• Triangle Calculator Right Arrow Icon
• Law of Cosines Calculator Right Arrow Icon
• Law of Sines Calculator Right Arrow Icon

Everyday Calculation

Free calculators and unit converters for general and everyday use.

Calculators » Math » Right Triangle

Right Angle Triangle Calculator

Our online tools will provide quick answers to your calculation and conversion needs. On this page, you can solve math problems involving right triangles. You can calculate angle, side (adjacent, opposite, hypotenuse) and area of any right-angled triangle and use it in real world to find height and distances.

Enter any two values and press calculate to get the other values

Angle A (degree):

Angle B (degree):

Download: Use this right-triangle solver offline with our all-in-one calculator app for Android and iOS .

Right triangle calculation

Formulas used for calculations on this page:

Pythagoras' Theorem a 2 + b 2 = c 2

Trigonometric functions: sin(A) = a/c, cos(A) = b/c, tan(A) = a/b sin(B) = b/c, cos(B) = a/c, tan(B) = b/a

Area = a*b/2, where a is height and b is base of the right triangle.

Related Calculators

• Mean, Median, Mode
• Area converter
• Length converter
• Area calculator
• Fraction calculator

© everydaycalculation.com

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Right Triangle Calculator

Right triangle calculator

Input any two values for a right triangle, and the calculator will find the unknown element. The calculator provides a step-by-step explanation on how to calculate missing elements. The calculator gives you a step-by-step guide on how to find the missing value.

• Factoring Polynomials
• Polynomial Roots
• Synthetic Division
• Polynomial Operations
• Graphing Polynomials
• Simplify Polynomials
• Generate From Roots
• Simplify Expression
• Multiplication / Division
• Addition / Subtraction
• Rationalize Denominator
• Simplifying
• Quadratic Equations Solver
• Polynomial Equations
• Solving Equations - With Steps
• Solving (with steps)
• Quadratic Plotter
• Factoring Trinomials
• Equilateral Triangle
• Right Triangle
• Oblique Triangle
• Square Calculator
• Rectangle Calculator
• Circle Calculator
• Hexagon Calculator
• Rhombus Calculator
• Trapezoid Calculator
• Triangular Prism
• Distance calculator
• Midpoint Calculator
• Triangle Calculator
• Graphing Lines
• Lines Intersection
• Two Point Form
• Line-Point Distance
• Parallel/Perpendicular
• Circle Equation
• Circle From 3 Points
• Circle-line Intersection
• Modulus, inverse, polar form
• Vectors (2D & 3D)
• Add, Subtract, Multiply
• Determinant Calculator
• Matrix Inverse
• Characteristic Polynomial
• Eigenvalues
• Eigenvectors
• Matrix Decomposition
• Limit Calculator
• Derivative Calculator
• Integral Calculator
• Arithmetic Sequences
• Geometric Sequences
• Find n th Term
• Degrees to Radians
• Trig. Equations
• Long Division
• Evaluate Expressions
• Fraction Calculator
• Greatest Common Divisor GCD
• Least Common Multiple LCM
• Prime Factorization
• Scientific Notation
• Percentage Calculator
• Dec / Bin / Hex
• Probability Calculator
• Probability Distributions
• Descriptive Statistics
• Standard Deviation
• Z - score Calculator
• Normal Distribution
• T-Test Calculator
• Correlation & Regression
• Simple Interest
• Compound Interest
• Amortization Calculator
• Annuity Calculator
• Work Problems

Hire MATHPORTAL experts to do math homework for you.

Prices start at $3 per problem.

Right triangle calculations

The calculator uses the following formulas to find the missing values of a right triangle:

Example 01 :

Find hypotenuse $ c $ of a right triangle if $ a = 4\,cm $ and $ b = 8\,cm $.

When we know two sides, we use the Pythagorean theorem to find the third one.

Example 02 :

Find the angle $\alpha$ of a right triangle if hypotenuse $ c = 14~cm$ and leg $ a = 8~cm$.

In order to find missing angle we can use the sine function

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)

Right Triangle Calculator English Español

A right triangle is a geometrical shape in which one of its angle is exactly 90 degrees and hence it is named as right angled triangle. This right triangle calculator helps you to calculate angle and sides of a triangle with the other known values. You can select the angle and side you need to calculate and enter the other needed values.

Right Angled Triangle Calculator

Here is the online right triangle calculator for you to calculate any two parameters of the right angled triangle given the values for the remaining two known parameters. All the four parameters being angle, opposite side, adjacent side and hypotenuse side. A right triangle is a geometrical shape in which one of its angle is exactly 90 degrees. In the below online right triangle calculator, just select two parameters which you need to find, and submit to calculate angle and sides of a triangle. For side calculation, this right angled triangle calculator can accept only the angle equal to or below 90 degrees.

The formulae (formula) for calculating angle and sides of a triangle can be easily remembered using the sentence - O ld H arry A nd H is O ld A unt.

A right triangle with 5 cm as base and 10 cm as height, will have an hypotenuse value of     = √(5^2 + 10^2)     = √(25 + 100)     = √(125)     = 11.18 cm Substituting the hypotenuse and opposite side values in the Sin q formula, we have Sin q = 10 / 11.18     = 63.43 degrees

Related Articles:

• Table of sin, cos and tan values
• Different types of tri angles

Related Calculators:

• Half Angle Formula Calculator
• Triangle Law Of Forces
• Triangle Theorems Calculator
• Law Of Cosines Calculator
• Trigonometry Calculator Sin Cos Tan Inverse
• Double Angle Identity Solver, Formula - Trig Calculator

Calculators and Converters

• Calculators
• Trigonometry
• Trigonometric Angles

Top Calculators

Popular calculators.

• Derivative Calculator
• Inverse of Matrix Calculator
• Compound Interest Calculator
• Pregnancy Calculator Online

Top Categories

Right Triangle Angle And Side Calculator

No results found

We can’t find anything with that term at the moment, try searching something else.

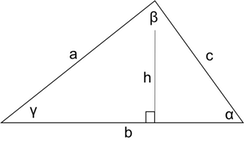
Triangle Calculator

The triangle calculator finds all triangle measurements – side lengths, triangle angles, area, perimeter, semiperimeter, heights, medians, inradius, and circumradius.

Related Calculators

There was an error with your calculation.

Table of Contents

Triangle calculator, directions for use, limitations on the input values, calculation example, triangle: definition and important formulas, conditions of existence of a triangle, triangle measurements.

The triangle calculator is an online triangle solver allowing you to find all triangle measurements based on three known measurements quickly. The calculator takes the lengths of the sides of a triangle and triangle angles as inputs and calculates the following measurements:

• missing side lengths,
• missing triangle angles,
• semiperimeter,
• heights to all sides of the triangle,
• medians to all sides of the triangle,
• circumradius.

The calculator also provides the coordinates of the vertices, the centroid, the inscribed circle center, and the circumscribed circle center, assuming that the coordinates of vertex A are [0, 0].

To use this triangle calculator, enter any three values into the input fields. You can enter the values of any angles or any side lengths. Note that at least one of the values has to represent a side length; otherwise, a triangle will have infinite solutions.

After entering the values, select the units for triangle angles. You can choose between degrees or radians. When selecting radians, use "pi" to represent π. For example, if the angle value is \$\frac{π}{3}\$, enter "pi/3." After inserting the known values, press "Calculate." The calculator will return all missing values from the list above and the schematic view of the triangle, which will help you better visualize it.

After the answer, you can expand the following field - Show Calculation Steps – to get familiar with the solution algorithm and the formulas used to find the answer.

At least one of the known values must be a side length.

When entering the following combination of values – two angles and one side length – note that the sum of the angle values has to be less than 180° or π.

When entering three side lengths, note that the sum of any two side lengths should be greater than the length of the remaining side.

Imagine you are moving and want to borrow a truck from a friend. You will need to load and unload the truck, but it doesn't have a built-in ramp. You have a portable ramp, but you must ensure its dimensions fit the truck's height. Your ramp is not adjustable, and you have measured that its two sides measure as 1 m and 0.8 m, and the angle opposite to the side of 1 m is 85 degrees (see the image). You know that you can adjust the truck's height from 0.5 m to 1 m. Does your ramp fit?

• side b = 1;
• side c = 0.8;
• angle B = 85 degrees.

To determine whether your ramp fits the truck, you need to solve the triangle above and estimate whether the length of side A fits the given range for the truck's height: 0.5< a < 1 .

Inserting the values presented above into the triangle calculator, you get the following answer in the task, we will only need the missing side length.

So the rest of the answers are not demonstrated in this practical example, while the triangle solver still calculates them:

Side a = 0.67376

Side c = 0.8

angle A = 42.16° = 42°9'35" = 0.73582 rad

angle B = 85° = 1.48353 rad

angle C = 52.84° = 52°50'25" = 0.92224 rad

The ramp looks something like this:

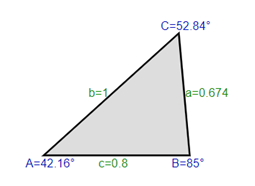
We see that a ≈ 0.674, and we know that the height of the truck can be adjusted in the range 0.5 < a < 1 . This means that the ramp height fits the adjustable height of the truck, and you can borrow the truck from your friend instead of renting one!

In geometry, a triangle is a plane figure made by the intersection of three straight non-parallel lines. A triangle can also be described as a polygon with three vertices and three edges. The edges of the triangle are usually called sides.

Two conditions define the existence of a triangle; one condition is applied on the sides, and the other – on the angles. The condition on the sides is based on the triangle inequality. It states that the sum of the lengths of any two sides of the triangle must be greater than or equal to the length of the remaining third side. If the sum of the lengths of the two sides equals the length of the third side, the triangle is called degenerate.

A degenerate triangle is a triangle where all three vertices lie on the same straight line. It's a very special triangle case, usually not discussed in elementary geometry, and is, therefore, not considered here.

The condition on the angles states that the sum of the three angles of any triangle always equals 180° or π radians.

Let's define the most crucial triangle measurements and look at the formulas for calculating their values.

The perimeter of a triangle is the sum of the lengths of all its sides and can be found as follows:

p = a + b + c

The semiperimeter of a triangle – is half of the length of the perimeter of the triangle:

$$s=\frac{p}{2}=\frac{a+b+c}{2}$$

The area of a triangle – is a property describing how much space the triangle takes up on a plane. If the lengths of the two sides of the triangle and the angle between these two sides are known, the area of a triangle can be calculated as follows:

$$A=\frac{1}{2}a× b×\sin{C}$$

A triangle's height, or altitude, is perpendicular from one of the angles to the opposite side. Since any triangle has three sides, any triangle will also have three perpendiculars. A height perpendicular to side A is usually denoted as hₐ . Similarly, the other two heights are denoted as \$h_b\$ and h꜀ . The easiest way to find the height of a triangle is through its area:

$$A=\frac{1}{2}× a× h_a=\frac{1}{2}× b× h_b=\frac{1}{2}× c× h_c$$

$$h_a=\frac{2A}{a}, h_b=\frac{2A}{b}, h_c=\frac{2A}{c}$$

Median to a side of a triangle – is the line from a vertex of the triangle to the middle of the opposite side. Any triangle has three medians.

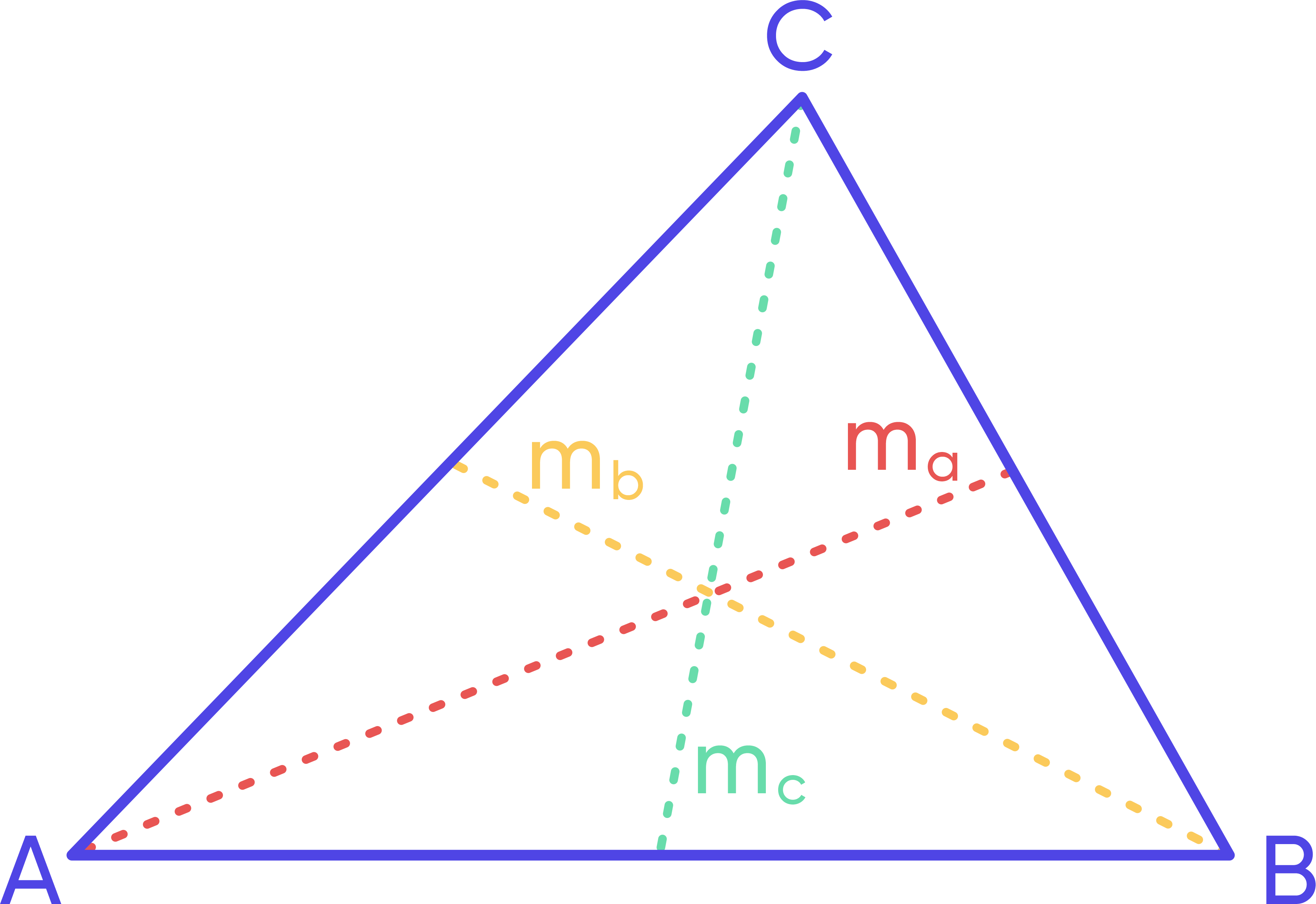
A median to side a is usually denoted as mₐ . Similarly, the other two medians are denoted as \$m_b\$ and m꜀ . We can find the lengths of the medians with the following formula:

$$m_a=\frac{1}{2}\sqrt{2b²+2c^2-a^2}$$

The inradius of a triangle – is the radius of a circle inscribed inside the triangle and touching all of its sides.

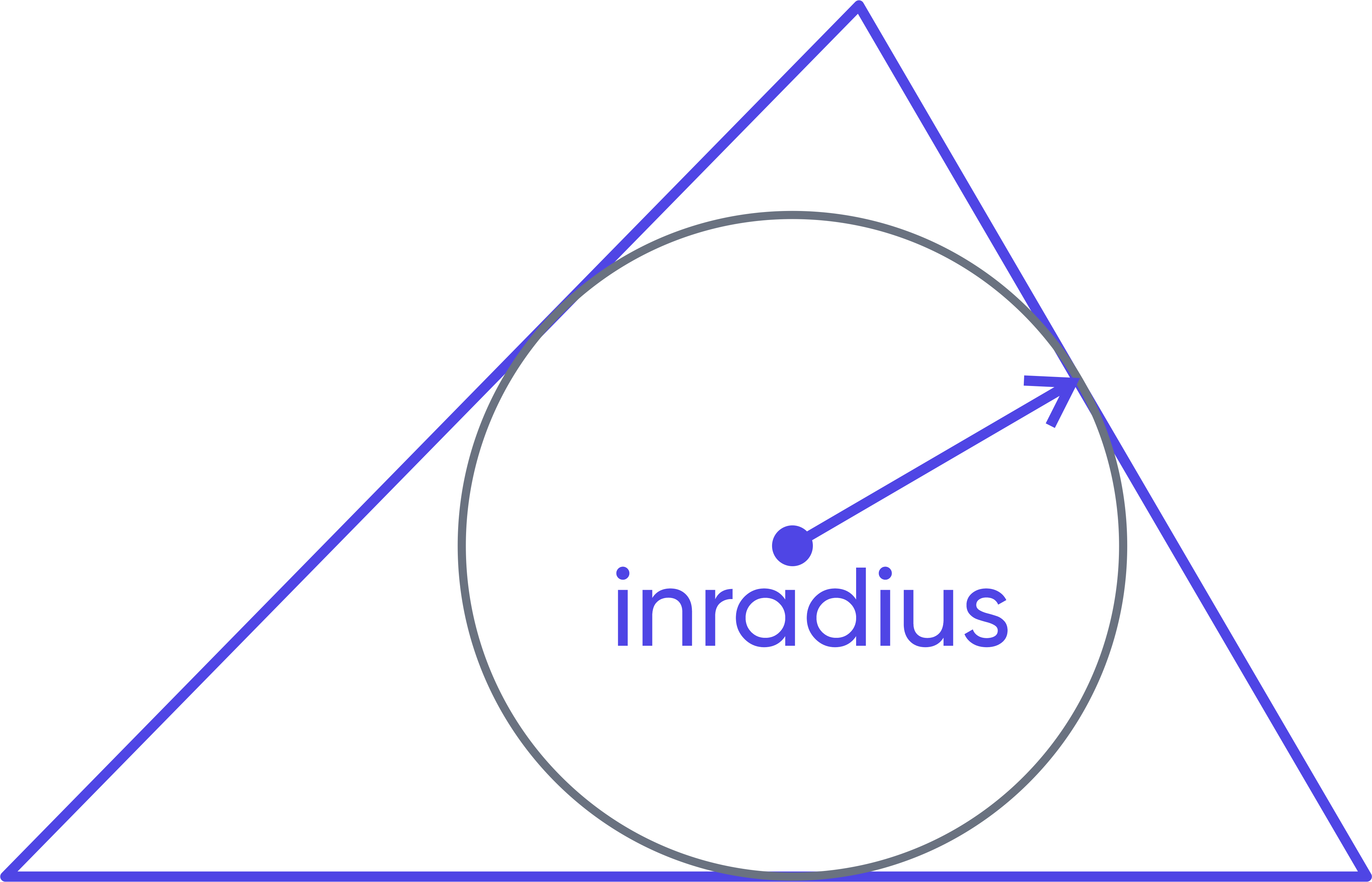
The length of the inradius r can be found as follows:

$$r=\frac{A}{s}$$

The circumradius of a triangle – is the radius of a circle passing through all three vertices of the triangle.

We can find the length of the circumradius R from the sine rule:

$$2R=\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}$$

The sine rule is also beneficial for finding the missing values of side lengths or angles of a triangle. Another helpful rule is the cosine rule:

$$a=\sqrt{b²+c^2-2bc\cos{A}}$$

$$b=\sqrt{a^2+c^2-2ac\cos{B}}$$

$$c=\sqrt{a^2+b²-2ab\cos{C}}$$

The formulas listed above allow calculating all triangle measurements. The triangle calculator uses these formulas to find the missing values.

Triangle Calculator

Enter the values of any two angles and any one side of a triangle below which you want to solve for remaining angle and sides.

Triangle calculator finds the values of remaining sides and angles by using Sine Law.

Sine law states that

a sin A = b sin B = c sin C

Cosine law states that-

a 2 = b 2 + c 2 - 2 b c . cos ( A ) b 2 = a 2 + c 2 - 2 a c . cos ( B ) c 2 = a 2 + b 2 - 2 a b . cos ( C )

Click the blue arrow to submit. Choose "Solve the Triangle" from the topic selector and click to see the result in our Trigonometry Calculator!

Solve the Triangle

Popular Problems-

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Triangle calculator

How does this calculator solve a triangle.

• The expert phase is different for different tasks. The calculator tries to calculate the sizes of three sides of the triangle from the entered data. He gradually applies the knowledge base to the entered data, which is represented in particular by the relationships between individual triangle parameters. These are successively applied and combined, and the triangle parameters are calculated. Calculator iterates until the triangle has calculated all three sides. For example, the appropriate height is calculated from the given area of the triangle and the corresponding side. From the known height and angle, the adjacent side, etc., can be calculated. The calculator uses use knowledge, e.g., formulas and relations like the Pythagorean theorem, Sine theorem, Cosine theorem, and Heron's formula.
• The second stage is the calculation of the properties of the triangle from the available lengths of its three sides.

Examples of how to enter a triangle:

Triangles in word problems:.

Look also at our friend's collection of math problems and questions:

• right triangle
• Heron's formula
• The Law of Sines
• The Law of Cosines
• Pythagorean theorem
• triangle inequality
• similarity of triangles
• The right triangle altitude theorem

• Calculate Δ by 3 sides SSS
• Δ SAS by 2 sides and 1 angle
• Δ ASA by 1 side and 2 angles
• Scalene triangle
• Right-angled Δ
• Equilateral Δ
• Isosceles Δ
• Δ by coordinates
• List of triangles

Trig Triangle Calculator

Right triangle trigonometry, using two sides for right triangle trigonometry calculation, using one angle and one side for right triangle trigonometry calculation, using area and one side for right triangle trig calculation, other trigonometry and triangle calculators.

If you're dealing with trigonometry and right triangles, this trig calculator for right triangles is here for you. This tool uses trigonometry to calculate these triangles, as long as you know:

• Two of its sides;
• One angle and one side; or
• The area and one side.

To learn more, keep reading this article that briefly discusses the trigonometry behind right triangles.

This trig triangle calculator uses the following widely-known trigonometric ratios, which relate the sides of a right triangle to its angles:

🙋 To know how to calculate or evaluate the sine, cosine, and tangent functions, visit our trig calculator .

Additionally, we can use the inverse trigonometric functions to solve for the angles if we know the length of the sides:

🙋 To know how to calculate or evaluate these inverse functions, visit our inverse sine , inverse cosine , and inverse tangent calculators .

Let's use the following triangle to explain how this calculator solves for the different sides and angles according to the information known.

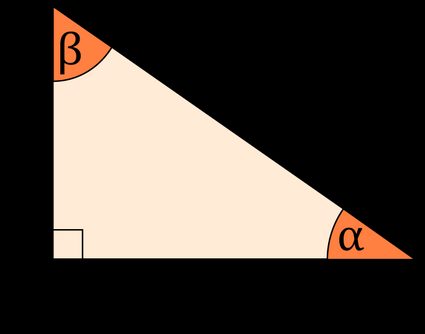
Finding the third side

If you know two sides, the easiest way to find the third side is by using the Pythagorean theorem ( what is the Pythagorean theorem ).

• Given a and b: c = a 2 + b 2 c = \sqrt{a^2 + b^2} c = a 2 + b 2 ​ ;
• Given a and c: b = c 2 − a 2 b = \sqrt{c^2 - a^2} b = c 2 − a 2 ​ ; and
• Given b and c: a = c 2 − b 2 a = \sqrt{c^2 - b^2} a = c 2 − b 2 ​ .

Finding the angles

Then, we can find α \alpha α or β \beta β by taking any of the inverse trigonometric functions mentioned previously:

Finding the angle

The sum of the internal angles of a triangle will always be 360 ° 360\degree 360° . In a right triangle , there's a right angle ( 90 ° 90\degree 90° ) and, therefore, the sum of the other two angles ( α \alpha α and β \beta β ) will be 90 ° 90\degree 90° . Therefore:

• Given β \beta β : α = 90 ° − β \alpha = 90\degree - \beta α = 90° − β ; or
• Given α \alpha α : β = 90 ° − α \beta = 90\degree - \alpha β = 90° − α

Finding the two missing sides

To find the two unknown sides, you can use the angle α \alpha α and the trigonometric ratios:

Given a : c = a / sin ⁡ α c = a/{\sin{\alpha}} c = a / sin α and b = a / tan ⁡ α b = a/{\tan{\alpha}} b = a / tan α ;

Given b : c = b / cos ⁡ α c = b/{\cos{\alpha}} c = b / cos α and a = b × tan ⁡ α a = b \times {\tan{\alpha}} a = b × tan α ; and

Given c : a = c × sin ⁡ α a = c \times \sin{\alpha} a = c × sin α and b = c × cos ⁡ α b = c \times {\cos{\alpha}} b = c × cos α ;

If you know a a a or b b b , use the right triangle area formula that relates the base ( b b b ) to the height ( a a a ) and solve for the unknown side:

• Given a: b = 2 × Area / a b = 2 \times \text{Area}/a b = 2 × Area / a ; and
• Given b: a = 2 × Area / b a = 2 \times \text{Area}/b a = 2 × Area / b .

Once you know at least two sides, use the second section method to obtain the angles.

• Trigonometry calculator ;
• Cosine triangle calculator ;
• Sine triangle calculator ;
• Right triangle trigonometry calculator ;
• Sine cosine tangent calculator ;
• Tangent ratio calculator ; and
• Tangent angle calculator .

What's the leg measurement of a 45-45-90 triangle of 18 cm hypotenuse?

If the hypotenuse of a 45-45-90 triangle measures 18 cm, the length of any of its two legs is 9√2 cm or 12.728 cm . To get to this answer:

Take the sin of any of the 45° angles, which equals any of the legs ( a ) divided by the hypotenuse ( c ):

sin(45°) = a / c

Solve for the leg ( a ): a = c × sin(45°)

Remember that sin(45°) = 1/√2 and input the hypotenuse c = 18 cm : a = 18 cm × (1/√2) : = 9/√2 cm = 12.728 cm

What's the leg measurement of a 45-45-90 triangle of 10√5 inches hypotenuse?

If the hypotenuse of a 45-45-90 triangle measures 10√5 inches, the length of any of its two legs is 5√10 inches or 15.81 inches . To get to this answer:

You can use the formula that relates the hypotenuse ( c ) to any of the legs ( a ) of a 45-45-90 triangle: c = a × √2

And solve for the leg a :

a = c /√2 = (10√5 in)/√2 = 5√10 in = 15.81 in.

• Trig Identities Calculator

Flat vs. round Earth

Partial fraction decomposition, plant spacing, triangle similarity.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (570)
• Health (440)
• Physics (510)
• Sports (105)
• Statistics (184)
• Other (183)
• Discover Omni (40)

• Calculators
• Triangle...

Triangle Calculator

Please provide values for any three of the six fields below. At least one of those values must be a side length.

Hello there!

About the Triangle Calculator

This triangle calculator lets you solve a triangle. It calculates the missing measurements of a triangle if you know any one side and any two from the remaing five mesurements.

The calculator will give you not just the answers, but also a step-by-step solution.

Usage Guide

I. valid inputs.

The triangle calculator requires exactly three of the six inputs — one side-length and any two of the remaining inputs.

The inputs themselves must be non-negative real numbers and can be in any format — integers, decimals, fractions, or even mixed numbers. Here are a few examples.

• Whole numbers or decimals → 2 \hspace{0.2em} 2 \hspace{0.2em} 2 , − 4.25 \hspace{0.2em} -4.25 \hspace{0.2em} − 4.25 , 0 \hspace{0.2em} 0 \hspace{0.2em} 0 , 0.33 \hspace{0.2em} 0.33 \hspace{0.2em} 0.33
• Fractions → 2 / 3 \hspace{0.2em} 2/3 \hspace{0.2em} 2/3 , − 1 / 5 \hspace{0.2em} -1/5 \hspace{0.2em} − 1/5
• Mixed numbers → 5 1 / 4 \hspace{0.2em} 5 \hspace{0.5em} 1/4 \hspace{0.2em} 5 1/4

Finally, of course, the inputs shouldn't violate any of the properties of triangles. For example, sum of angles must not exceed 180 ° \hspace{0.2em} 180 \degree \hspace{0.2em} 180° .

ii. Example

If you would like to see an example of the calculator's working, just click the "example" button.

iii. Solutions

As mentioned earlier, the calculator won't just tell you the answer but also the steps you can follow to do the calculation yourself. The "show/hide solution" button would be available to you after the calculator has processed your input.

We would love to see you share our calculators with your family, friends, or anyone else who might find it useful.

By checking the "include calculation" checkbox, you can share your calculation as well.

Here's a quick overview of what it means to solve a triangle and a few related concepts to help you make sense of the solutions provided by the triangle calculator.

For those interested, we have a more comprehensive tutorial on solving triangles .

Solving a Triangle

There are six values describing the six parts of a triangle — three sides and three angles. Now, if we know one side and any two of the other five values, we can use that information to find the remaining three.

Finding the unknown measurements of a triangles from what is known is referred to as solving triangles .

Important Concepts

Let's look at a few of the important concepts that help us solve triangles.

Angle Sum Property

The sum of the three internal angles of a triangle is 180 ° \hspace{0.2em} 180 \degree 180° .

The sine rule states that the ratio of side length to the sine of opposite angle is the same for all sides in a triangle.

Triangles Calculator

Calculate area, perimeter, sides and angles for triangles step-by-step.

• Basic (Linear)
• Biquadratic
• Logarithmic
• Exponential
• Solve For x
• Scientific Calculator
• Scientific Notation Arithmetics
• Complex Numbers
• Cartesian to Polar
• Polar to Cartesian
• System of Inequalities
• Partial Fractions
• Periodicity
• Y Intercept
• X Intercepts
• Point Slope Form
• Step Functions
• Arithmetics
• Start Point
• Area & Perimeter
• Sides & Angles

Law of Sines

Law of cosines.

• Width & Length
• Volume & Surface
• Edges & Diagonal
• Volume & Radius
• Surface Area
• Radius & Diameter
• Volume & Height
• Circumference
• Eccentricity
• Trigonometric Equations
• Evaluate Functions

Equilateral

Isosceles Triangle

Right Angled

triangles-calculator

Related Symbolab blog posts

Please add a message.

Message received. Thanks for the feedback.